こちらの記事はDIVXアドベントカレンダー2022の12日目の記事です。

はじめに

こんにちは。DIVXエンジニアの黒石です。主にWebアプリケーションの脆弱性診断業務を担当しています。

今回のテーマは暗号化に関係する言葉の使い方です。

暗号化の反対は復号“化”？

1つ目は復号“化”です。
よくネットワークやセキュリティに関する書籍のコラム等で触れられているので、知っている方にとっては「ああアレね」という感じかもしれません。

結論から言うと“暗号化”の対義語は“復号”です。“化”はつきません。対称性がなくて気持ち悪いですね。

「そういうもん」で片付けてしまっても良いのですけど、今回はちょっとだけ言葉の意味を深掘りしてみます。

“〇〇化”は“〇〇に変えること”

まず“〇〇化”について考えます。

“〇〇化”は“〇〇に変えること”を意味します。ここで〇〇にはモノや状態を表す言葉が入ります。

これを踏まえた上で“暗号”と“復号”という2つの熟語の構成を考えてみます。

“暗号”は“暗い号”というモノ

次に“暗号”について考えます。

“暗号”は1文字目が2文字目を修飾するパターンの熟語です。つまり“暗い号”という構造です。
“暗”はどんなという修飾で、本体は“号”というモノです。

“暗い号”だと抽象的過ぎて説明が乱暴なので、それぞれの漢字の解釈も補足します。

ここでの“暗”は光が弱い様子から転じて“見えない”や“分からない”といった意味と考えられます。

そして、“号”は“信号”や“記号”等での使われ方と同様に“取り決めに従って表現された情報”といったところでしょう。

“復号”は“号を復する”という動作

一方“復号”はどうでしょうか？

“復号”は1文字目が動作で2文字目が目的語というパターンの熟語です。つまり“号を復する”という構造です。
本体は“復”という元に戻す意味の動作で、“号”は何をか示す目的語です。

“化”を付けたら

最後に“暗号”と“復号”それぞれに“化”を付けるとどんな意味になるか考えてみます。

“暗号”に“化”を付けると“暗号に変えること”という意味になります。“暗号”はモノなので自然ですね。

一方“復号”は元に戻す動作なので、“〇〇に変えること”に入れるのは不自然だと分かります。
いわゆる“頭痛が痛い”と同様とも言えます。“□□が痛い”の□□には“体の部位”を入れるべきなのに、“痛み”である“頭痛”を入れてしまっているという、有名な間違いです。（ちなみに同じ漢字が続くことが問題ではないです。例えば“歌を歌う”は正しい日本語です。）

復号“化”の違和感

こうして“復号”という言葉の意味を考えてみると復号“化”の違和感が分かると思います。

ただし、言葉は少しずつ変化していくものです。最近だと自動翻訳により日本語化された文章（海外製品のドキュメント等）で復号“化”を目にします。使われる頻度が増えていけば、復号“化”も正しい言葉とされるかもしれません。

（余談）復号“化”が辞書に載っていないからか、“ふくごうか”の変換ミスで“複合化”になっている文章も度々見かけます。これは流石に論外だと思ってます。

Base64は“暗号”？

2つ目はBase64に関するお話です。

先に言うとBase64は“暗号”ではありません。

しかし私は、弊社に転職する前、Base64エンコーディングすることを“暗号化する”と言うエンジニアさんに何度か遭遇しました。中にはエンジニア歴2桁年の方もいらっしゃったので、混同している中堅〜ベテランの方も多いかもしれません。

そもそもBase64とは？

Base64は64種類（※）の文字を使ってバイナリデータを表現する技術です（※厳密にはパディング用の文字=も含めて65種類）。

64は2の6乗なので64種類の文字を使えば1文字あたり6ビット分の情報を表せます。4文字で3バイト（24ビット）分の情報です。

具体的には、0〜25は大文字アルファベット（A〜Z）、26〜51は小文字アルファベット（a〜z）、52〜61は数字（0〜9）、62は+、63は/、と対応します。

なお3バイトずつ変換するので、元データのバイト数が3の倍数でない場合は、3の倍数になるように残りのバイトを0でパディングします。そしてパディングした値のみのブロックは=で表します。

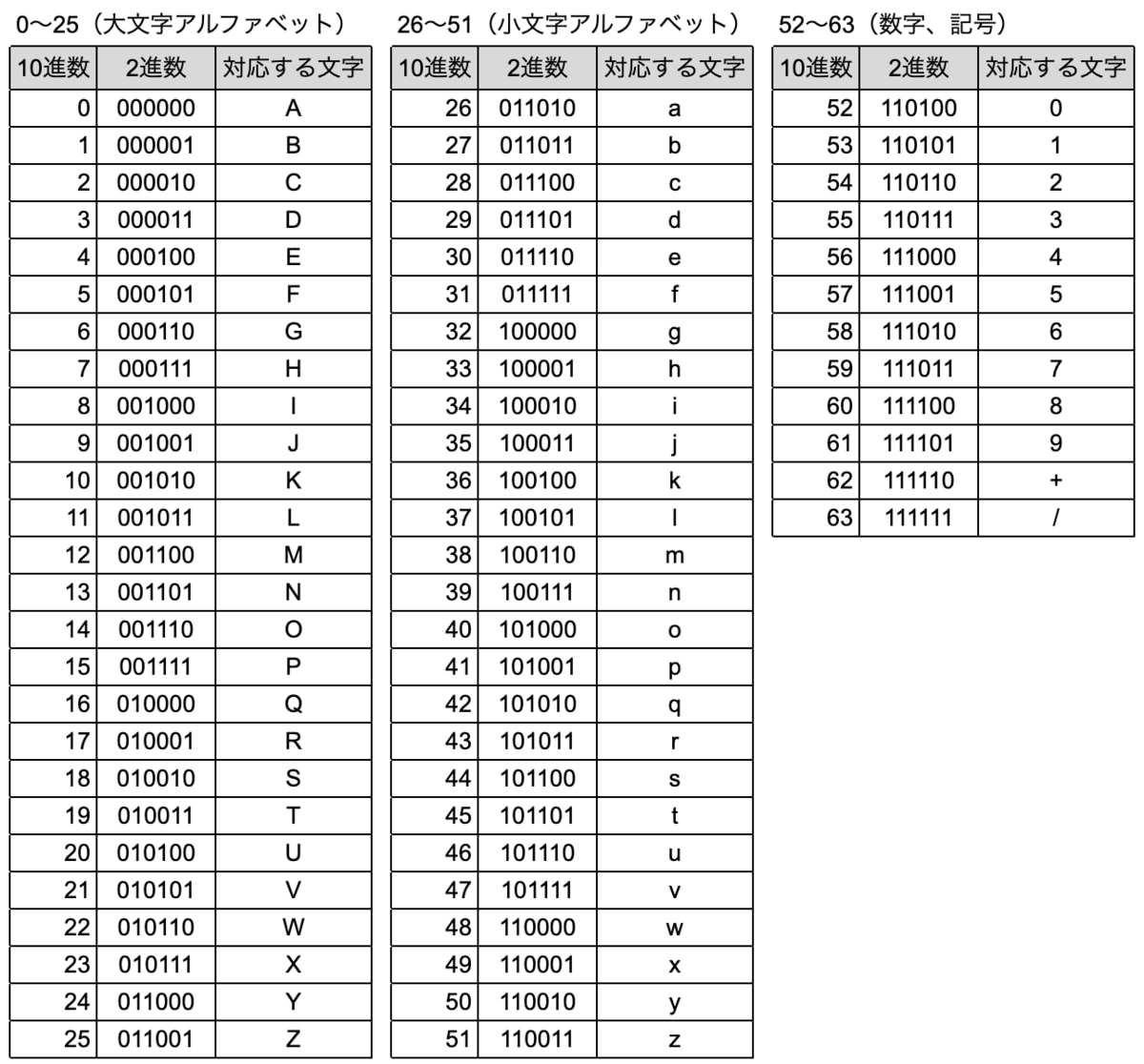
Base64変換表Base64エンコーディングの例

言葉だけだとイメージしにくいので実際にやってみます。例として下記の10バイトの2進数（16進数で48656c6c6f2044495658）をBase64エンコーディングします。

01001000 01100101 01101100 01101100 01101111 00100000 01000100 01001001 01010110 01011000

3バイト毎の処理イメージ

最初の3バイト（01001000 01100101 01101100）の処理イメージです。
まず6ビットずつの4ブロックに分割します。010010、000110、010101、101100となります。（人間が見やすいように10進数も併記しておきます。それぞれ18, 6, 21, 44です。）

次に各ブロックに対応する文字を割り当てます。010010はS（大文字）、000110はG、010101はV, 101100はs（小文字）ですね。

これで3バイトのバイナリデータ（01001000 01100101 01101100）をSGVsという4文字に変換できました。

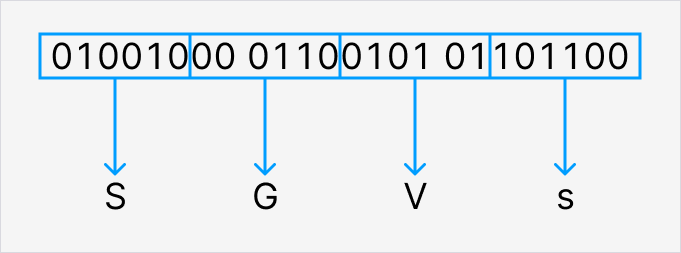
Base64エンコーディングイメージ（最初の3バイト）

同様の手順で、4〜6バイト目（01101100 01101111 00100000）はbG8gに、7〜9バイト目（01000100 01001001 01010110）はRElWに変換できます。

端数バイトの処理イメージ

今回の元データは10バイトなので、3バイトずつ処理した結果、最後に端数の1バイト（01011000）が残っています。

まずは3バイトになるように末尾を0でパディングします。01011000 00000000 00000000となります。

次に、先ほどと同様に6ビットずつの4ブロックに分割します。010110、000000、000000、000000となります。（10進数だとそれぞれ22, 0, 0, 0です。）このとき2ブロック目の末尾4ビットと3, 4ブロック目はパディングで追加した情報です。

最後に各ブロックに対応する文字を割り当てます。010110はW（大文字）、000000はAです。ただし3ブロック目と4ブロック目は元データに存在しない情報なので=で表します。（2ブロック目は先頭2ビットが元データの情報なので通常通りAです。）

これで末尾の1バイト（01011000）もWA==に変換できました。

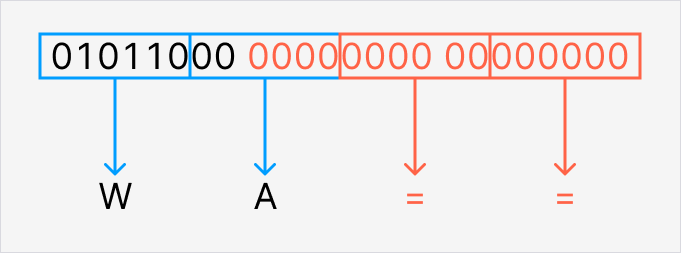
Base64エンコーディングイメージ（端数の1バイト）

エンコーディング結果

以上の処理で全体のエンコーディング結果はSGVsbG8gRElWWA==となりました。

ちなみに16文字なので、元データの単純な16進数表記（48656c6c6f2044495658で20文字）に比べて少ない文字数で情報を表現できています。

Base64デコーディングの例

こんどはBase64デコーディングもやってみます。例として先ほどのエンコーディング結果（SGVsbG8gRElWWA==）を対象とします。

基本的な変換

基本的には、S→010010、G→000110、……と各文字に対応する6ビットに変換していくだけです。（4文字ずつ変換すると24ビット＝3バイト分の元データになるのでキリが良いです。）

ただし、最後だけはパディング処理によって元データに存在しない情報が混ざっている場合があるので注意が必要です。

パディングのパターン

Base64エンコーディングは3バイトずつ行うので、パディングのパターンは以下の3つです。

• 元データのバイト数が3で割ると2余る数：パディングが1バイト分必要です。1バイトは6ビット＋2ビットなので、=（6ビット全てがパディング情報の文字）は1つとなり、=を除いた最後の文字は末尾2ビットがパディング情報となります。
• 元データのバイト数が3で割ると1余る数：パディングが2バイト分必要です。2バイトは6ビット＋6ビット＋4ビットなので、=は2つとなり、=を除いた最後の文字は末尾4ビットがパディング情報となります。
• 元データのバイト数が3で割り切れる数：このパターンはパディングが発生せず=はありません。

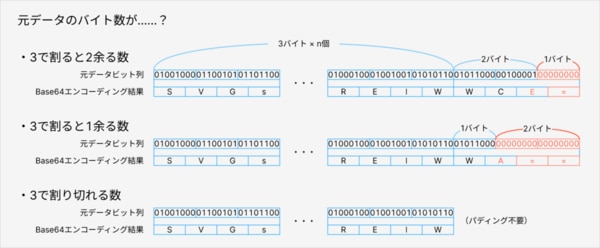
パディングのパターン

以上から、=の数によりどこからがパディングされた情報か分かります。

今回の場合、=が2つあるので元データのバイト数が3で割ると1余る数のパターンです。つまり=を除いた最後の文字（A）は末尾4ビットがパディング情報と分かります。A→000000なので末尾4ビットを無視して00だけ使います。

デコーディング結果

上記手順の結果、下記のビット列にデコーディングできました。

010010 000110 010101 101100 011011 000110 111100 100000 010001 000100 100101 010110 010110 00

分け目を6ビット毎から8ビット毎に直すと下記になります。これは最初のエンコーディング前のデータと一致しています。

01001000 01100101 01101100 01101100 01101111 00100000 01000100 01001001 01010110 01011000

Base64エンコーディングされた文字列は誰でも解読できますね

この通りBase64エンコーディングされた文字列は、誰でも（やり方さえ知っていれば）元のバイナリデータを取り出せます。
もし、なんとなくBase64を“暗号”と言っている方がいたら、本来暗号化して秘匿すべき情報をBase64エンコーディングしただけにしていないかちょっと心配です。

まとめ

今回は言葉の使い方について述べてきました。
ちなみに私の中では、今回のもう1つのテーマは好奇心でした。

「復号“化”」という言葉を見て「じゃあ“復号”って何だろう」と考えたり、Base64を使うとき「Base64のエンコーディングやデコーディングはどんな処理だろう」と調べたり、そういった好奇心が大事だと思うのです。

DIVXでは一緒に働ける仲間を募集しています。
興味があるかたはぜひ採用ページを御覧ください。